Upper bounds on packing density for circular cylinders with high aspect ratio
| Authors: | Wöden Kusner |
| Journal: | Discrete & Computational Geometry, 524964-978, 2014. |
| Full text: | arXiv • DOI |
Abstract:
In the early 1990s, A. Bezdek and W. Kuperberg used a relatively simple argument to show a surprising result: The maximum packing density of circular cylinders of infinite length in $\mathbb{R}^3$ is exactly $\pi/\sqrt{12}$, the planar packing density of the circle. This paper modifies their method to prove a bound on the packing density of finite length circular cylinders. In fact, the maximum packing density for unit radius cylinders of length $t$ in $\mathbb{R}^3$ is bounded above by $\pi/\sqrt{12} + 10/t$.
Comments and Corrigenda:
-
Section 1.4, paragraph 1: The only existing bounds for circular cylinders and capped cylinders of finite length are …
-
Section 1.4 paragraph 2: … both very close to where the bounds of Fejes Tóth and Kuperberg flatten
sout. -
Figure 3 displays the incorrect conjectured lower bound. It should appear as
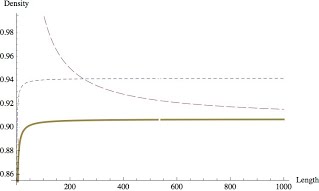
-
Section 3, paragraph 2: Define the Dirichlet slice $d_x$ to be the set …
-
References: Wilker, J.B.: $[$1987$]$ Problem II. Intuitive Geometry $($Siófok, 1985$)$, Colloq. Math. Soc. János Bolyai, vol. 48. North-Holland, Amsterdam New York, p.700